Глава «Пропорции в египетской архитектуре» книги «Всеобщая история архитектуры. Том I. Архитектура Древнего мира». Автор: В.Н. Владимиров; под редакцией О.Х. Халпахчьна (отв. ред.), Е.Д Квитницкой, В.В. Павлова, А.М. Прибытковой. Москва, Стройиздат, 1970

---

В построении пропорций возможны два основных метода.

1. Арифметические системы, где пропорции вычисляются абстрактным методом (по числам). Разновидностью этого способа является модульная система, при которой размер какой-либо части здания (например, диаметр колонны) принимается за единицу (модуль) и по отношению к нему все остальные размеры выражаются в простых числах.

2. Геометрические системы пропорций, где все три проекции сооружения определяются путем геометрических построений (чаще всего на основе квадрата или круга). Наибольшую роль здесь играет принцип подобия частей.

Частным случаем геометрических построений является группа отношений так называемого «золотого сечения» (т. е. деления отрезка в среднем и крайнем отношении), при котором весь отрезок так относится к большей своей части, как большая часть относится к меньшей. Таким образом, постоянная пропорция этой системы, образуя убывающую или возрастающую прогрессию, связывает воедино все элементы здания, от больших до самых малых величин.

Золотым сечением наиболее часто занимались теоретики, исходя из квадрата, точнее, из двух квадратов (Хембидж) или из деления окружности на десять частей (Мёссель).

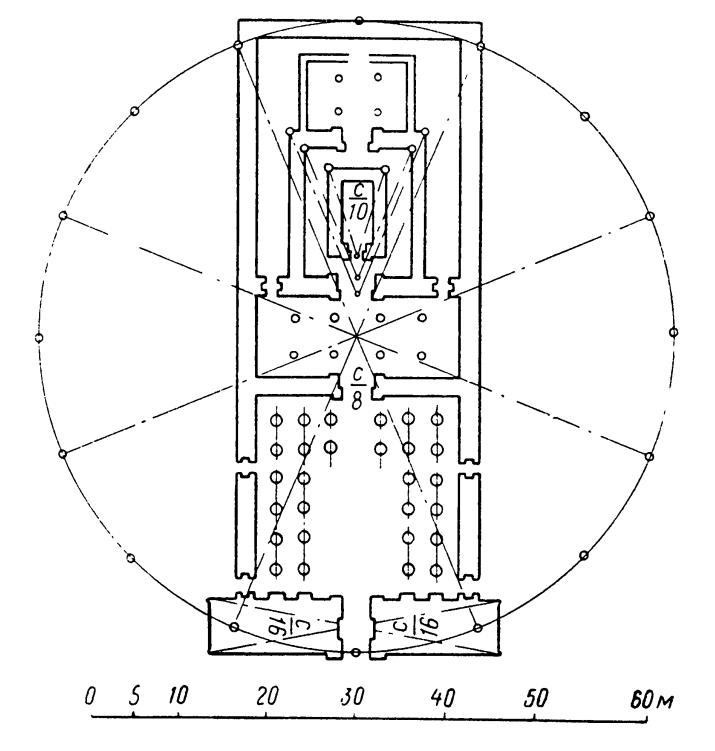
Оба названных исследователя приводят, кроме того, общие законы построений, объясняющие все схемы геометрических пропорций. Мёссель, например, выводит все геометрические фигуры из деления окружности на различное число частей. По Мёсселю пропорции храма Хонсу в Карнаке были определены путем вписывания его в круг (описанный веревкой на земле), разделенный на восемь частей (рис. 129).

Система пропорций, применявшаяся в архитектуре Древнего Египта, построена на квадрате и его производных (рис. 130). Эту систему построения ряда последовательно увеличивающихся производных квадрата мы будем называть в дальнейшем системой диагоналей.

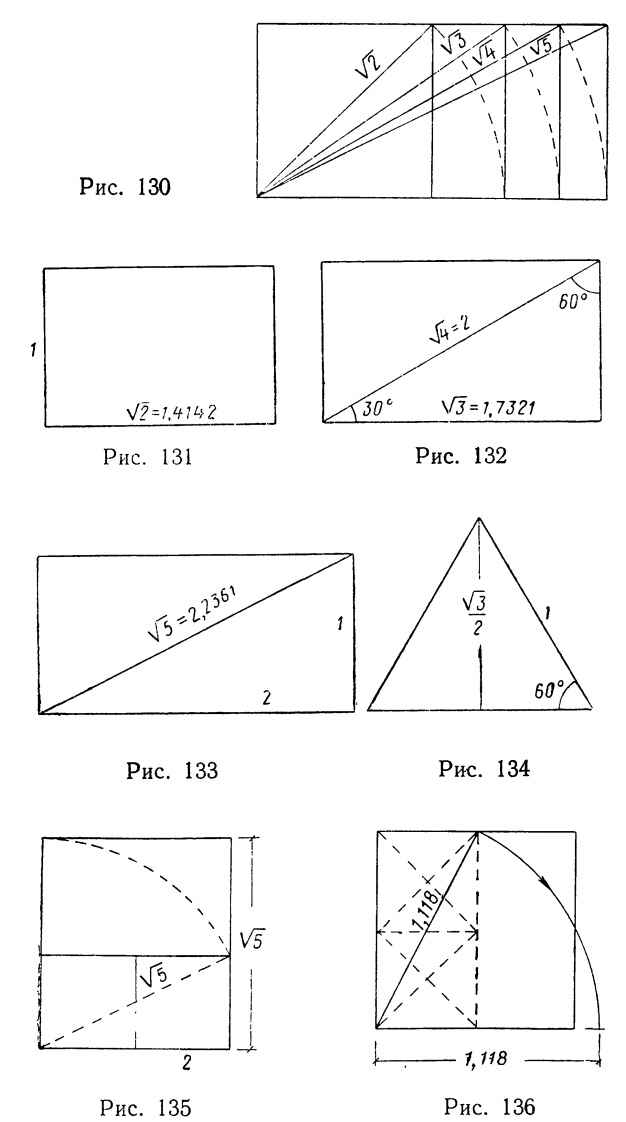
Эти четыре фигуры, связанные между собой общим построением, обладают интересными свойствами. Первая фигура — квадрат — одна из простейших фигур, имеющая равные стороны. Она является основной формой в ранней архитектуре Древнего Египта, так же как и связанная с ней вторая фигура — прямоугольник с отношением сторон, равным отношению стороны квадрата к его диагонали (рис. 131).

Отношение сторон в нем ^√2/₁ = 1,4142 или ¹/_√2 = 0,7071.

Третья фигура имеет отношение сторон ¹/_√3 = 0,5773 или ^√3/₁ = 1,7321.

Половина этого прямоугольника образует прямоугольный треугольник с меньшей стороной, равной половине гипотенузы, и с углами 30° и 60°. Хорошо знакомый всем угольник с такими углами является, вероятно, самым ранним вспомогательным прибором в работе архитектора, наравне с угольником, имеющим угол 45° и равным половине квадрата.

Отношение большего катета к гипотенузе в треугольнике с углом 60° равно ^√3/₂ = 0,866.

Четвертая фигура представляет собой прямоугольник, составленный из двух квадратов (рис. 133).

В нем примечательно часто встречающееся в Египте отношение диагонали к большей стороне ^√5/₂ = 1,11805, совпадающее с «функцией» золотого сечения. Отношение малого катета к диагонали ¹/_√5 = 0,4472.

Эти шесть связанных между собой величин:
1) квадрат;
2) его диагональ;
3) прямоугольный треугольник с углом 60°;
4) прямоугольник, состоящий из двух квадратов;
5) и 6) отношения его диагонали к сторонам ^√5/₂ и ^√5/₁ — лежат в основе пропорций большинства сооружений Древнего царства.

Иногда кроме квадрата применялся равносторонний треугольник (рис. 134).

Он имеет уже знакомое отношение высоты к стороне — ^√3/₂ : 1 = 0,866 или стороны к высоте 1 : ^√3/₂ = 1,155.

Все эти фигуры могут быть построены в натуре при помощи простой веревки. Даже прямоугольник с таким иррациональным и, казалось бы, сложным отношением сторон, как ^√5/₂ = 1,118, которое является отношением диагонали двух квадратов к стороне (рис. 135), может быть построен этим простейшим способом (такой прямоугольник условно называется в дальнейшем неточным квадратом).

Это же отношение может быть получено при помощи диагонали полуквадрата (рис. 136), так как половина квадрата составляет прямоугольник в два малых квадрата.

Система квадрата и его производных стала применяться, вероятно, еще в архаическом периоде. По этим пропорциям построен один из самых ранних египетских памятников — предполагаемая гробница фараона Менеса в Негаде, относящаяся к I династии (рис. 137).

Особенность описанной выше системы построения последовательно увеличивающихся прямоугольников при помощи диагоналей заключается в том, что большие величины (диагонали) оказываются производными от меньших величин — сторон квадрата или прямоугольника. Поэтому в ранних памятниках построение должно было идти от части к целому. Дионисий Галикарнасский, историк I в. до н. э., приписывает египетским скульпторам применение «аналогии от наименьшей [величины] до наибольшей».

Такой исходной величиной в гробнице Менеса служит ширина основной камеры, равная высоте равностороннего треугольника, вписанного в эту камеру. Половина этой меньшей стороны камеры будет модулем построения пропорций; обозначим ее буквой а. Интересен тот факт, что начальная фигура построения не является точным квадратом (²/_√3 = 1,155), хотя и очень близка к нему.

Этот прием будет иногда повторяться в последующих памятниках.

Все дальнейшее построение пропорций гробницы в Негаде основано только на квадратах.

Исходя из фигуры центральной камеры, легко построить пропорции среднего объема ИКМ₃Н₃, включающего пять внутренних камер. Центральная камера (в план которой может быть вписан равносторонний треугольник) окружена стенами, толщина которых равна половине ширины камеры, т. е. модулю а. Вся ширина центрального объема поэтому равна 4а. К полученному прямоугольнику ДБЖЗ с меньших сторон были прибавлены два точных квадрата — ЗЖМ₃Н₃ и ИКБД. В них заключено по две камеры, равные половине центральной; следовательно, в эти камеры вписываются прямоугольные треугольники с углом в 60°. Две из этих камер примыкают к стенам центральной камеры; положение двух крайних определено пересечениями их внешних углов с диагоналями квадратов.

Положение внешних стен определяется путем удвоения ширины центральной части плана — ИКМ₃Н₃. Общая ширина гробницы ПР (без постамента), таким образом, равна 8а. Внешние габариты ее близки к двум квадратам, но, как понятно из построения, отличаются от них в сторону удлинения на разность сторон центральной камеры. Габариты же постамента гробницы СТУФ равны точно двум квадратам. Ширина постамента определяется точками пересечения (X и Щ) диагоналей боковых квадратов среднего объема (ОЖ,0З и 0₁Б,0₁Д ).

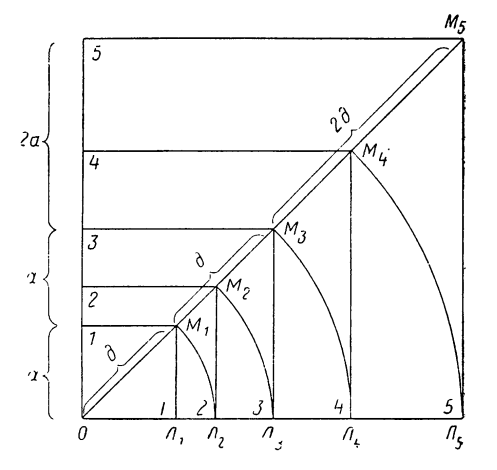
Непонятное на первый взгляд несовпадение толщины внешней стены с разбивочным модулем а указывает на то, что в данном случае наряду с методом кратного повторения модуля, применен какой-то иной способ построения пропорций. Этим способом является, вероятно, метод последовательно увеличивающихся квадратов, представляющий известную аналогию с описанным выше (рис. 130) способом построения по системе диагоналей. Сущность этого метода пояснена на рис. 138. В основу построения положен квадрат №1. Его диагональю ОМ₁ как радиусом, производится засечка на оси абсцисс (и ординат). Из за сеченной точки Л₂ восстанавливается перпендикуляр, который отсекает на линии диагоналей (на биссектрисе) отрезок ОМ₂, являющийся диагональю квадрата №2. Затем радиусом ОМ₂ повторяется засечка оси абсцисс, определяющая точку Л₃, и т. д. В этом построении сторона каждого последующего квадрата относится к стороне предыдущего, как диагональ квадрата к его же стороне, т. е. как ^√2/₁. Так же относятся друг к другу и диагонали последовательных квадратов:

ОЛ₂/ОЛ₁ = ОЛ₃/ОЛ₂ = ОЛ₄/ОЛ₃ = ОЛ₅/ОЛ₄ = ... = ^√2/₁
ОМ₂/ОМ₁ = ОМ₃/ОМ₂ = ОМ₄/ОМ₃ = ОМ₅/ОМ₄ = ... = ^√2/₁

Откуда
ОЛ₃ = 2ОЛ₁ ; ОЛ₅ = 2ОЛ₃;
ОМ₃ = 2ОМ₁; ОM₅ = 2ОM₃.

Поскольку
OЛ₂ = OЛ₁ (√2)¹
ОЛ₃ = ОЛ₁ (√2)² = 2ОЛ₁;
ОЛ₄ = ОЛ₁ (√2)³ = ОЛ₂ х 2√2;
ОЛ₅ = ОЛ₁ (√2)⁴ = 4ОЛ₁

Из указанных равенств видно, что метод последовательного построения квадратов дает при двукратном применении удвоение размера, откуда вытекает совпадение найденных этим методом угловых точек М₃ и М₅ с точками пересечения соответствующих линий стен (рис. 137), построенных способом повторного отложения (удвоения) модуля а, как описано выше. Метод последовательно увеличивающихся квадратов дает, однако, помимо точек М₃ и М₅ также и точку М₄, которая определяет ширину внешнего кольца камер и, следовательно, толщину наружной стены. Точка М₂ остается неиспользованной.

Таким образом, система модульных кратных отношений сочетается с методом последовательно построенных квадратов и с системой диагоналей (или иррациональных величин). Примитивную модульность раннего Египта нельзя признать развитой системой арифметических кратных отношений; она сводится к простым удвоениям величин, вытекающим из употребления указанных двух способов пропорционального построения, дающих последовательно то целые, то иррациональные величины.

Из остальных пропорциональных зависимостей в гробнице в Негаде следует отметить равенство расстояния между осями выступов фасада и толщины внешней стены. Так, построение фасада связывается со всеми остальными размерами плана. Вертикальные пропорции фасада трудно определить, так как гробница сохранилась плохо.

В такой законченной системе квадратов обращает на себя внимание появление неквадратной формы в основе всего построения пропорций. Этот факт легко объясняется приемами построения прямого угла. В условиях примитивной техники восстановление в натуре перпендикуляра к прямой возможно только методом засечек при помощи веревок. Применявшийся позднее «священный» египетский треугольник со сторонами 3 : 4 : 5 , служивший, по Плутарху, египтянам для построения прямого угла, в ранних памятниках не обнаруживается.

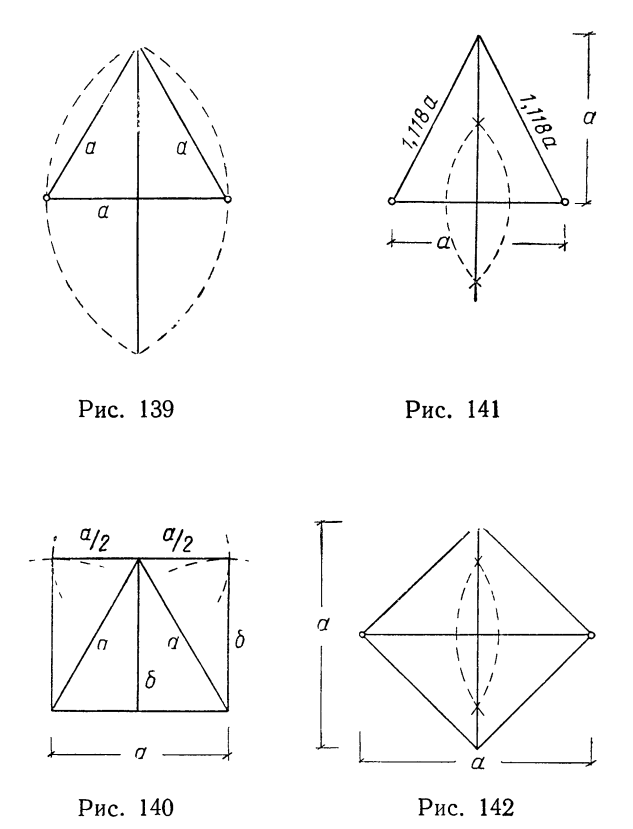
При построении засечками перпендикуляра к прямой возможны три различных итога.

1. Если мы примем для радиуса засечек заданное расстояние между исходными точками построения а , то в результате получим равносторонний треугольник (139).

Построив засечками около одного из углов равностороннего треугольника две его половины, мы получим прямоугольник с отношением сторон ^а/_б = ^1,155/₁ (рис. 140)

Таким методом и построены пропорции центральной и боковых камер гробницы в Негаде.

2. Если мы берем произвольные радиусы, то на полученном перпендикуляре можно отложить заданное расстояние а двумя способами.

Отложив отрезок а полностью вверх, получим треугольник с высотой а и основанием а. Его стороны будут в этом случае равны 1,118 а (оис. 141).

Отношение ¹/_1,118 определяет пропорцию второй, весьма часто применявшейся формы построения центральной части здания или ансамбля.

3. Третий результат получится, если отложить на перпендикуляре заданный отрезок а таким образом, чтобы его середина совпала с основной прямой. Тогда мы получим квадрат, но он окажется повернутым в неудобное для дальнейшего построения положение (рис. 142).

Наблюдаемое в гробнице Менеса употребление двух частично совпадающих между собой систем пропорционирования — метода удвоений и системы диагональных (иррациональных) отношений — характерно для всего раннего периода Древнего Египта.

Ясно также, что на ранней стадии египетской архитектуры проблема пропорций была нераздельно связана с проблемой измерения и разбивки здания в натуре и, вероятно, возникла на основе практики строительства (значение квадрата обусловливалось тем, что он служил мерой площади).

Можно утверждать, что сознательно применяемая пропорциональная закономерность была методом художественного построения уже в искусстве времени I династии.

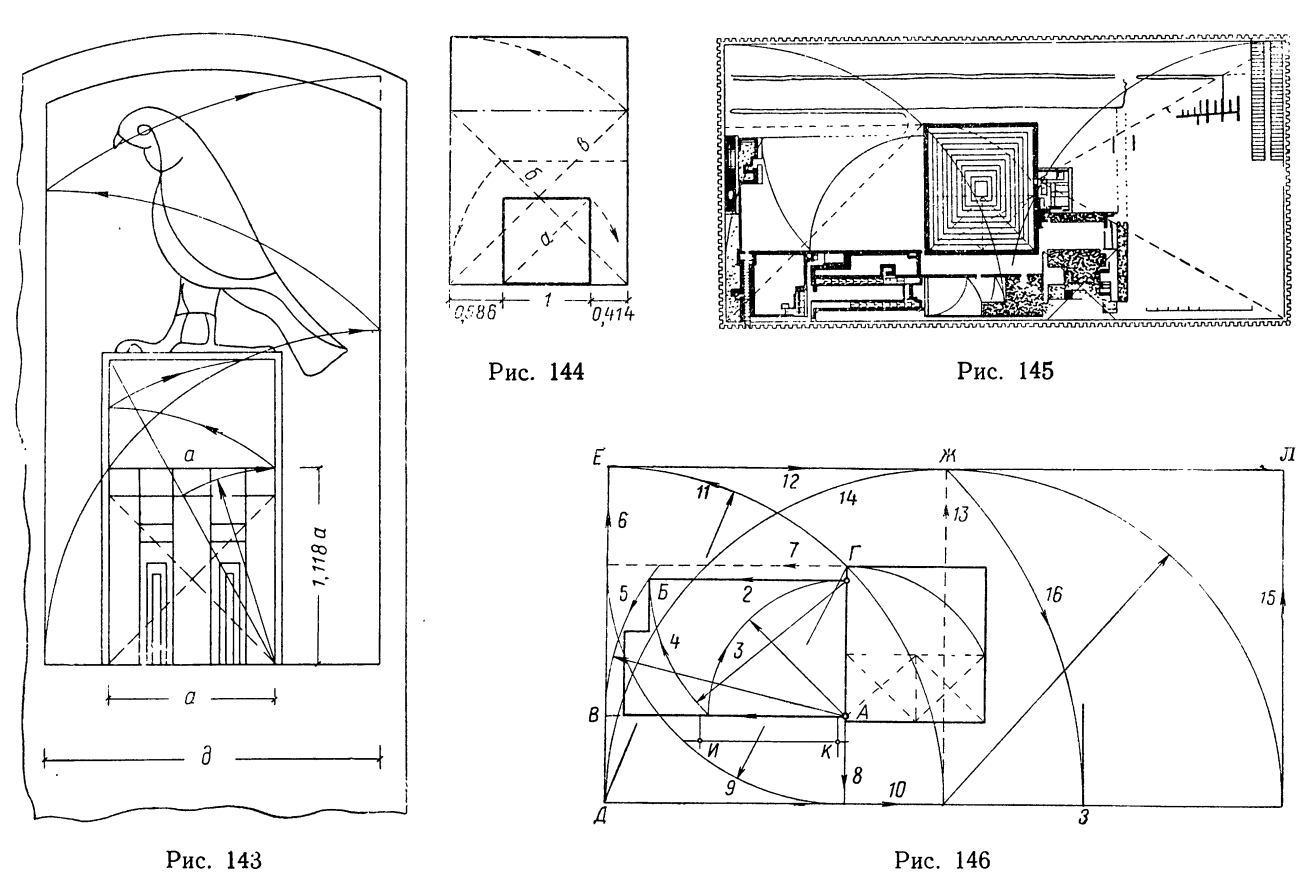
Построение пропорций по диагоналям четко обнаруживается в рельефе мемориальной стелы фараона Джета в Абидосе (рис. 143). В нем центральное изображение — фасад дворца — вписано в квадрат, отмечающий низ украшений, и в прямоугольник ¹/_1,118 определяющий верхнюю грань дворца (рис. 136). Рамка, окружающая дворец и эмблему, получена тремя засечками диагоналей из середины верхней стороны основного квадрата; отношение сторон в ней равно ¹/_1,802. Диагональ этой рамки равна внутренней ширине обрамления всей стены, высота которой, полученная двумя засечками, дает отношение катетов треугольника с углом в 60°.

На примере стелы фараона Джета можно видеть три свойства пропорций, применявшихся в Древнем Египте.

Первое: построение посредством диагоналей проводится с полной последовательностью: конечная величина, полученная в меньшей форме, переходит в большую форму как ее меньший размер.

Второе: пропорции в ранних памятниках берутся по внутренним обрезам стен или рамок. Это объясняется, вероятно, тем, что исходной пропорцией была пропорция интерьера, которую толщина стены своей добавкой нарушала (вскоре, впрочем, начали пропорционироваться и наружные размеры).

Третье: в Древнем царстве основная фигура часто смещается с оси внешнего прямоугольника по принципу, указанному на рисунке 144.

В стеле фараона Джета применено смещение основного квадрата по горизонтали (т. е. первые два построения на рис. 144).

В ансамбле Джосера в Саккаре (III династия) применены те же, очевидно, уже ставшие узаконенными, пропорции.

Исходной формой построения плана является центральная пирамида Джосера. Она сохранила архаическое неравенство сторон плана, заимствованное у мастабы. Отношение сторон ее плана 120 м : 107 м = 1,121. Оно отличается всего на 0,003 от «неточного квадрата» с отношением сторон ^√5/₂=^2,236/₂=^1,118/₁ (см. рис. 135 и 136).

Все дальнейшие пропорции ансамбля, так же как и пропорции основания пирамиды, построены на производных квадрата.

Цифры на чертеже указывают последовательность проведения линий (прямых и кривых) при построении чертежа.

К длинной южной стороне пирамиды со стороны главного входа примыкает большой двор, ширина которого равна узкой стороне пирамиды, т. е. исходной величине построения. Засечка диагонали квадрата, построенного на ширине двора (засечка 4), отсекает длину двора до выступа южной гробницы (до точки Б). Засечка диагонали полученного прямоугольника АБ (засечка 5) определяет положение внутренней поверхности стены, окружающей весь ансамбль (точка В). Диагональ квадрата (ГД), построенного на последней величине (засечка 11), отсекает общую ширину ансамбля (БД).

Фасад Южного дворца находится на средней оси всего ансамбля. Прямоугольник внешних стен ансамбля по их внутреннему габариту составляет два квадрата, а одна из диагоналей (ДЛ) этого прямоугольника проходит почти через центр пирамиды (прямоугольник внешних стен по наружному габариту дает случайную пропорцию: ^{544,9 м}/_{277,6 м} = 1,98).

Обращает на себя внимание сходство с этим построением построения гробницы в Негаде. Здесь также в основании пропорций лежит форма, близкая к квадрату, а наружный габарит гробницы состоит из двух квадратов. Но промежуточное построение по диагонали в ансамбле Саккары значительно сложнее. Равносторонний треугольник внутренней камеры гробницы в Негаде заменен здесь другим построением, дающим результат, близкий к пропорциям гробницы.

Правда, равносторонний треугольник встречается и в ансамбле Саккары. Он фиксирует положение северной стороны пирамиды, причем сторона этого равностороннего треугольника равна ширине всего ансамбля.

Пропорции почти всех остальных элементов генерального плана ансамбля в Саккаре построены также с применением квадрата и его производных. Так, отношение сторон широкой части двора Южного дворца равно отношению диагонали квадрата к его стороне, а двор по всей своей длине вместе с узкой его частью составляет два квадрата и т. д.

Величина основного модуля — ширина ступенчатой пирамиды — повторяется в длинах некоторых подчиненных частей, например двора хеб-сед (ИК).

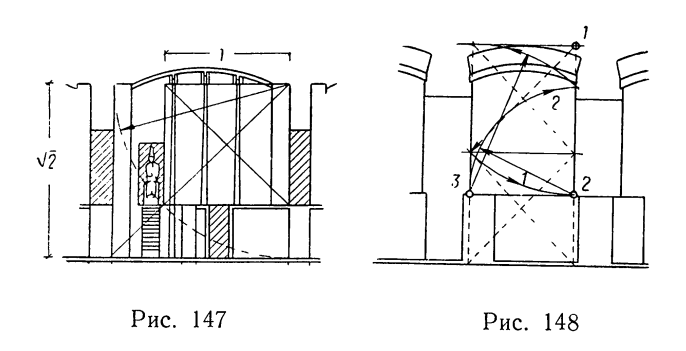
Фасады ряда сооружений ансамбля в Саккаре также подчинены пропорциям, построенным на производных квадрата. Так, некоторые фасады часовен на западной стороне двора хеб-сед вписываются в квадрат и имеют внутренние членения по принципу отношения стороны квадрата к его диагонали (рис. 147, левая сторона). Фасады ряда часовен противоположной, восточной стороны двора вписаны в два вертикально поставленных квадрата, причем пропорции верхней части каждой из них построены в отношении стороны квадрата и его диагонали (рис. 148).

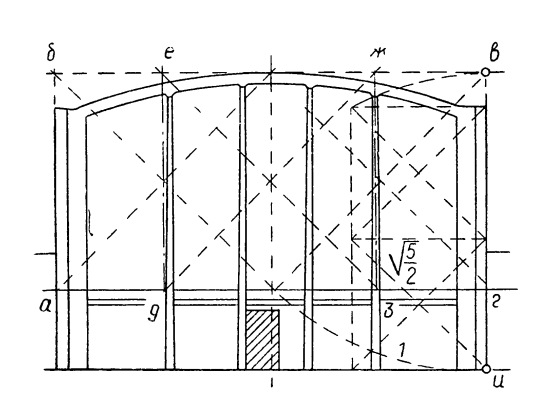
Более сложно сделан фасад Южного дворца (рис. 149). В нем верхняя часть, находящаяся над членящей стену лентой узора, вписана в два квадрата (абвг). Такой же квадрат (дежз) определяет положение внешних сторон декоративных средних полуколонн. Диагональ этих квадратов дает всю высоту гробницы с цоколем (засечка 1). Вся высота гробницы относится к высоте боковых устоев как ^√5/₂ (диагональ двух квадратов к большой стороне составленного из них прямоугольника).

Те же отношения применены в разрезе главного входа. Правда, к реставрированным высотам следует относиться с большой осторожностью.

Сама пирамида имеет отношение высоты к длине основания, равное 1 : 2 , а ее уступы уменьшаются кверху равномерно на одинаковую величину (около полуметра); тут применена простая арифметическая  прогрессия [Высота ступеней, начиная снизу (в м): 11,48; 10,95; 10,43; 9,92; 9,39; 8,89].

В итоге мы видим, что в ансамбле Саккары достигнуты поразительное единство и последовательная связанность пропорций, причем значительно меньшую роль, чем в архитектуре периода I династии, играют простые удвоения. Как общая композиционная схема, так и пропорции носят следы большого мастерства архитектора Имхотепа.

Следует отметить, что в египетских сооружениях, как показывают археологические обмеры, иногда наблюдается неточность разбивки углов в натуре. Например, в том же ансамбле Саккары коридор главного входа не параллелен наружной боковой стене. Грубая ошибка в разбивке прямого угла видна также в плане Рамессеума.

Однако, несмотря на эту неточность, почти во всех элементах ансамбля в Саккаре наблюдается единообразие пропорций, основанных на применении квадрата и его производных.

Ансамбль пирамид в Гизе, относящийся ко времени IV династии, скомпонован в единую группу. Все пирамиды довольно точно расположены по странам света почти параллельно одна другой. Трудность точного измерения пирамид (почти полное разрушение облицовки и непостоянный уровень песка) приводит к сильно различающимся у разных авторов размерам (так, высота пирамиды Хеопса указывается в отдельных случаях с разницей в 2 м). Поэтому при анализе пропорций здесь необходима особая осторожность.

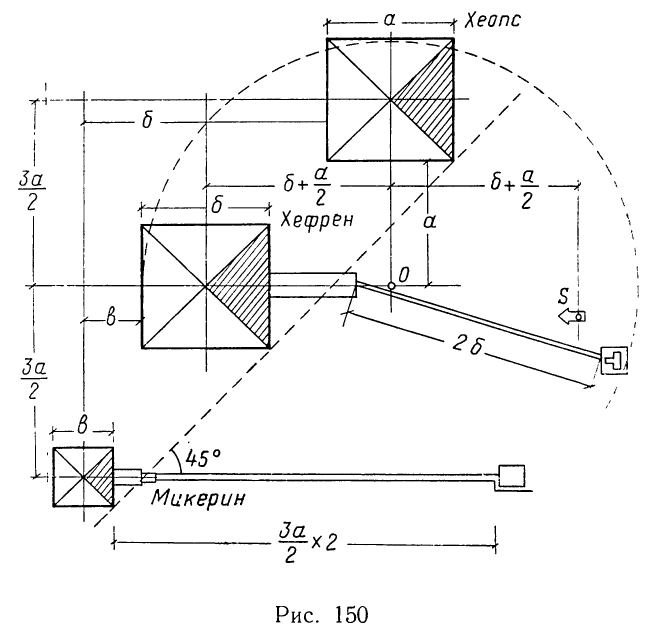
В построении общего плана ансамбля наблюдаются простые отношения: равенства и половины (рис. 150). Так, расстояние от угла пирамиды Хеопса до центра пирамиды Хефрена, находящегося почти на продолжении диагонали пирамиды Хеопса, равно этой диагонали. Если провести координаты, параллельные сторонам (и странам света), через центры всех трех пирамид ансамбля, то окажется, что по линии север — юг расстояния между центрами пирамид одинаковы, причем эти расстояния равны 3/2 стороны пирамиды Хеопса (^За/₂ на рисунке 150, левая сторона). Точка пересечения координат О получена (при разбивке плана пирамиды Хефрена) откладыванием от первой пирамиды точно на юг размера, равного стороне пирамиды Хеопса, а. При постройке же последней пирамиды (Микерина) уже заданное расстояние между вершинами было просто повторено.

Центр каждой следующей пирамиды по горизонтальной координате отстоит от основания предыдущей на расстоянии, равном стороне своего собственного основания (с очень небольшой неточностью).

Сторона основания пирамиды Микерина (с ошибкой меньше 0,5%) равна половине стороны основания пирамиды Хефрена (в = ^б/₂). Как меньшая пирамида Микерина выдвинута вперед по координате запад — восток, так что юго-восточные углы всех трех пирамид находятся почти на одной прямой.

По координате запад — восток голова большого сфинкса и вершина пирамиды Хефрена находятся на равных расстояниях от точки пересечения координат О. Расстояние от того же центра О до конца пирамиды Хефрена равно расстоянию от этого центра до конца выдвинутого вперед преддверия верхнего храма при пирамиде Хефрена. Длина крытого хода к преддверию равна удвоенной стороне пирамиды (2б). Также равенством определяется расстояние от пирамиды Микерина до ее выдвинутого на восток преддверия; это расстояние равно расстоянию между вершинами крайних пирамид по основной координате — север — юг (^3а/₂ х 2).

Пропорции пирамид в Гизе близки между собой. Разрезы всех пирамид дают приблизительно одинаковое отношение высоты к стороне основания и сходный угол наклона боковых сторон, равный у пирамиды Хеопса 51° 20', у пирамиды Хефрена 50° 20' и у пирамиды Микерина 51°. Высота и сторона основания пирамиды Хеопса — 146,59 и 230,35 м, а по другим данным — 148,2 и 232,8 м, Хефрена — 143,5 и 215,25 м; Микерина — 66,4 и 108,04 м.

В литературе имеется утверждение, что высота пирамиды Хеопса, относится к стороне ее основания как 2 : 3, т. е. разрез пирамиды будто бы составлен из двух связанных «египетских треугольников» с соотношением сторон 3 : 4 : 5, где высота пирамиды равна 4, а половина основания равна 3. Это утверждение не вполне соответствует фактическим данным. В действительности отношение этих величин равно: ^230,35/_2х146,59 = 0,785 или ^232,805/_2х148,2 = 0,785
вместо 0,75 (с большой ошибкой во втором знаке).

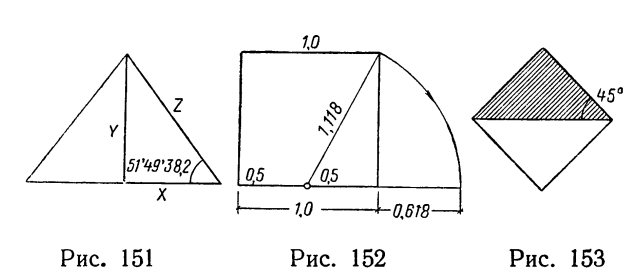
На наиболее близких к фактическим размерам пирамиды Хеопса данных основано предположение Прейса, что стороны полутреугольника поперечного сечения пирамиды (рис. 151) образуют геометрическую прогрессию, в которой ^Z/_Y = ^Y/_X (1)

Отношение между гипотенузой Z и малым катетом X равно φ (т. е. 1,618 ( 1 )).
^Z/_X =  φ = 1,618
откуда:
^Z/_Y = ^Y/_X = √ φ = 1,272
так как:
^Z/_X = φ; ^Z/_X x ^X/_Y = φ x ^X/_Y; ^Z/_Y = φ x ^X/_Y
Подставляя вместо ^X/_Y (1) равное ему отношение ^Y/_Z, получаем
^Z/_Y = φ ^Y/_Z; (^Z/_Y)² = φ;  ^Z/_Y = φ.

Если подставить реальные размеры в первую пропорцию, то получится действительно верный результат.

В пирамиде Хефрена отношение высоты к стороне основания составляет 2 : 3, причем эта пропорция выдержана математически правильно:  ^{143,5 м}/_{215,25 м} = 0,66.

Поэтому разрез пирамиды Хефрена может быть построен из двух сложенных треугольников с отношением сторон 3 : 4 : 5, где величина 4 соответствует высоте. При таком предположении пирамиду Хефрена можно считать самым ранним памятником, в котором появляются пропорции египетского треугольника.

В пирамиде Микерина отношение высоты к стороне основания ^66,4/_108,04 = 0,614 — величина, близкая к отношению золотого сечения — 0,618. Это первое появление отношения золотого сечения.

Частое пользование диагональю полуквадрата в ранней египетской архитектуре неминуемо должно было привести к открытию пропорций золотого сечения ¹/_0,618. (рис. 152)

Все описанные пропорции обнаруживаются в поперечном разрезе пирамид. Однако более вероятным представляется следующий способ определения их пропорций.

В папирусе Ринд, предположительно относимом к Древнему царству, есть задачи на построение пирамид. В них связываются три величины, относящиеся к диагональному разрезу через пирамиду по противоположным ребрам: диагональ основания пирамиды, сторона ребра и угол между ними. Требуется по любым двум данным из этих трех величин найти третью.

Возможность решения этих задач позволяет сделать вывод, что построение пропорций пирамиды основывалось на диагональном разрезе. В простейшем случае это построение можно представить себе таким образом: если мы разрежем квадрат по диагонали и половину его загнем на вертикальную плоскость, то получим диагональный разрез пирамиды, для которого весь квадрат является основанием (рис. 153). Такой идеальный случай не встречается при построении пирамид (везде их высота меньше половины диагонали основания), но все же они могли быть построены по тому же методу.

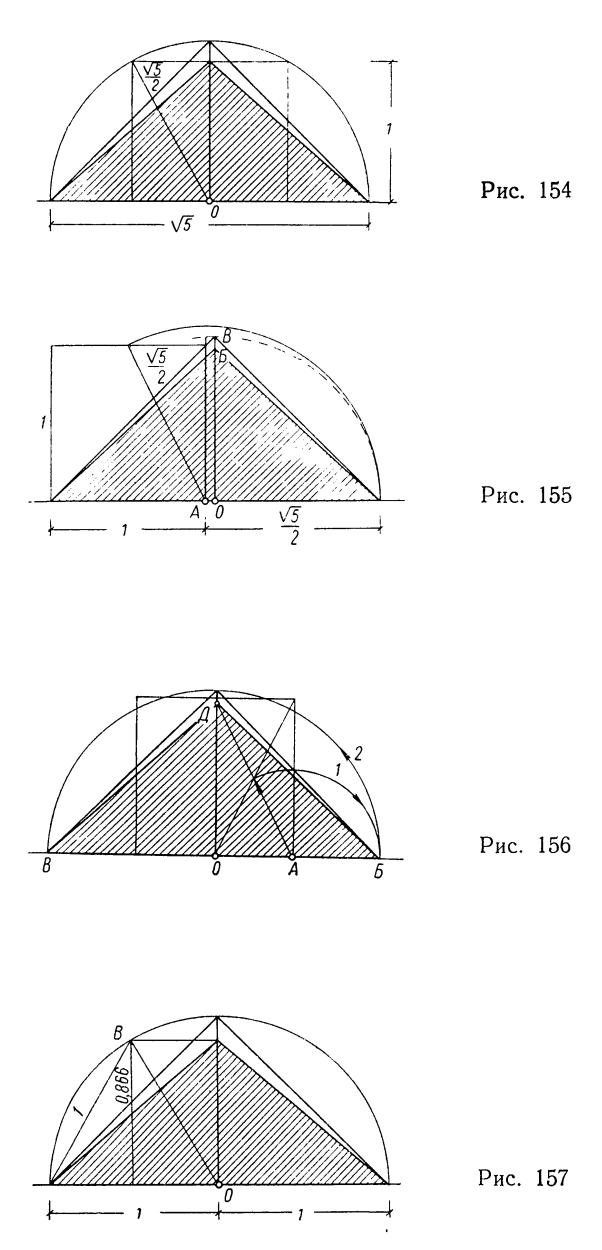
Пропорции пирамиды Хеопса, самой ранней из пирамид в Гизе, довольно точно определяются следующим построением (рис. 154).

Допустим, что на песке начерчен квадрат со стороной, равной высоте пирамиды Хеопса. Радиусом, равным диагонали полуквадрата (^√5/₂),из точки О очертим полуокружность до пересечения ее с продолженным основанием квадрата. Полученные крайние точки соединим со средней точкой верхней стороны квадрата и с верхней точкой полуокружности. Заштрихованный внутренний большой треугольник, переведенный в вертикальную плоскость, явится диагональным разрезом пирамиды Хеопса, а треугольник, доходящий вершиной до полуокружности, будет половиной основания этой пирамиды.

Реальные размеры исключительно точно соответствуют этому построению. Диагональ основания пирамиды Хеопса (при стороне в 230,35 м) равна 325,71 м. Отношение высоты к диагонали ^146,59/_325,71 =  0,45. Отношение же высоты пирамиды к диагонали ее основания в построении на рисунке равно ¹/_√5 = 0,4472. Эти величины не совпадают всего на 0,003; а «отклонения менее 0,002 - 0,003, — как говорит известный исследователь пропорций Мёссель, — не могут быть избегнуты в процессе строительства и оформления, так же как и при последующем обмере».

Интересно отметить, что те же пропорции, только с еще большей точностью повторяет впоследствии пирамида фараона Сахура (V династия). При высоте 49,6 м и стороне основания 78,32 м, диагональ ее основания будет равна 110,74 м. Отношение высоты к диагонали 110,74 : 49,6 = 0,448 отклонение от ¹/_√5 только 0,0005).

В таком построении примечательно, вопервых, то, что манипуляции с иррациональными величинами производятся простейшим способом при помощи примитивных приспособлений. Во-вторых, интересен прием одновременного вспомогательного построения плана и разреза здания на горизонтальной поверхности (земле). При таком способе достигается полная увязка величин и пропорций сооружения по всем трем координатам. В-третьих, примечательно применение построения, которое служит для определения пропорций золотого сечения, хотя самого отношения ¹/_0,618 здесь нет (см. рис. 152). Вероятно предположение, что появление пропорций золотого сечения относится к периоду IV династии.

Аналогичный метод применен и при построении остальных пирамид.

Пирамида Хефрена построена также по производным квадрата. Но диагональ его половины засечена от края квадрата (на рисунке 155 от точки А вправо), а не от середины, как в предшествующих случаях. Из средней точки основания пирамиды О восстановлен перпендикуляр, определяющий вершину пирамиды (Б — на продолжении верхней горизонтали квадрата) и угол плана (В — на продолжении диагонали квадрата или в точке пересечения перпендикуляра с полуокружностью). Заштрихованный внутренний треугольник является диагональным разрезом пирамиды. Те же результаты могут быть получены следующим построением (рис. 156). Из крайней точки А исходного квадрата радиусом, равным половине диагонали полуквадрата, засекается крайняя точка Б диагонали пирамиды. Радиусом ОБ описывается полуокружность до точки В. Соединение точек Б и В с точками Г и Д определит половину основания и диагональный разрез пирамиды. При указанных построениях получается отношение высоты разреза к основанию:

1/1+^√5/₂ = 1/1+1,118 = 1/2,118 = 0,4721

Реальная величина этого отношения в пирамиде Хефрена (при стороне в 215,25 м, высоте 143,50 м и вычисленной диагонали 304, 36 м) будет: ^143,5/_304,36 = 0,4714 (отклонение на 0,0007, много меньше допустимого).

Эта величина соответствует малой функции золотого сечения.

Важная роль отношения 0,472 для построения пирамиды Хефрена подтверждается тем, что то же отношение определяет основные пропорции плана преддверия храма при пирамиде Хефрена, выдвинутого вперед.

Пирамида Микерина построена с применением другой исходной фигуры — равностороннего треугольника. Полукруг описан вокруг одного из углов этого треугольника АВО радиусом, равным его стороне (рис. 157). Высота равностороннего треугольника равна высоте пирамиды. Отсюда отношение высоты к диагонали основания пирамиды равно: ^0,866/₂ = 0,433.

Реальная величина этого отношения в пирамиде Микерина (при высоте 66,4 м, стороне основания 108,04 м и диагонали 152,77 м) составит ^66,4/_152,77 = 0,43 (отклонение в 0,002 ).

В дальнейшем, при V династии, фактические пропорции планов в сооружениях Абусира почти совпадают с пропорциями, определяемыми построением по системе диагоналей и методу последовательных квадратов.

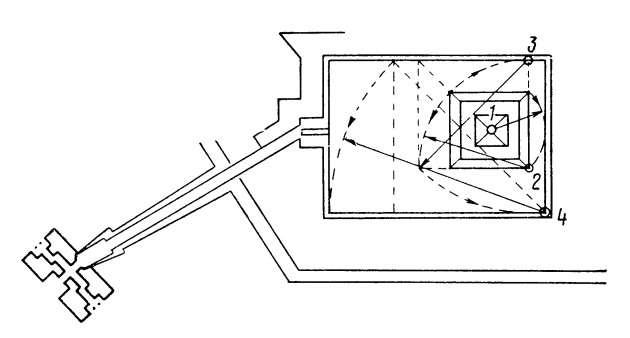
План храма солнца в Абусире (рис. 158) представляет пример смещения исходной фигуры в общем габарите ансамбля (построение произведено последовательными засечками из точек 1 ,2 ,3 и 4; см. рис. 144).

Ввиду плохой сохранности памятников архитектуры Среднего царства трудно определить характер пропорций этого времени. Более вероятно, что установленные в Древнем царстве приемы пропорционирования преобладали и в этот период.

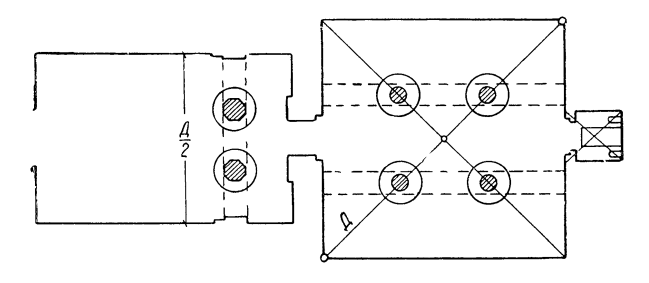
Гробницы Бени-Хасана, имеющие в ряде случаев неточность в углах и прямых линиях, построены явно на квадрате (рис. 159). Так, в гробнице Аменемхета квадрат определяет размеры внутреннего зала и задней камеры, а ширина входной части равна половине диагонали зала.

В архитектуре Нового царства помимо использования квадрата, применяемого даже в планировках городов (например, «восточный квартал» в Тель-эль-Амарне имеет размеры сторон 69 x 69,6 м, а земельные участки в нем 5 х 10 м), широко применялся также способ пропорционирования при помощи простых чисел. Обычно этот способ совмещался с диагональными построениями.

Дионисий Галикарнасский, историк I в. до н. э., приписывает египетским скульпторам применение модульных пропорций. По его словам, они «пользуются (одной и той же) аналогией от наименьшей (величины) до наибольшей, Создавая симметрию (соразмерность) живого существа путем разделения всей величины его тела на 21¼ части».

В связи с этим утверждением обращает на себя внимание египетский папирус времени XVIII династии, изображающий фасад киоска, вписанный в сетку, состоящую по высоте из 21 клетки, по ширине из 14 клеток. Основные членения киоска совпадают с делениями сетки или с серединами этих делений. Верхнее украшение киоска слегка выходит за пределы сетки; возможно, что это не случайное совпадение с указанным у Дионисия разделением фигуры «живого существа» на 21¼ части.

Несомненно, что египетские архитекторы пользовались приемом числового модуля. В Новом царстве весьма часто обнаруживается кратность размеров частей здания. Модулем обычно служит ширина святилища, иногда взятая вместе со стенами.

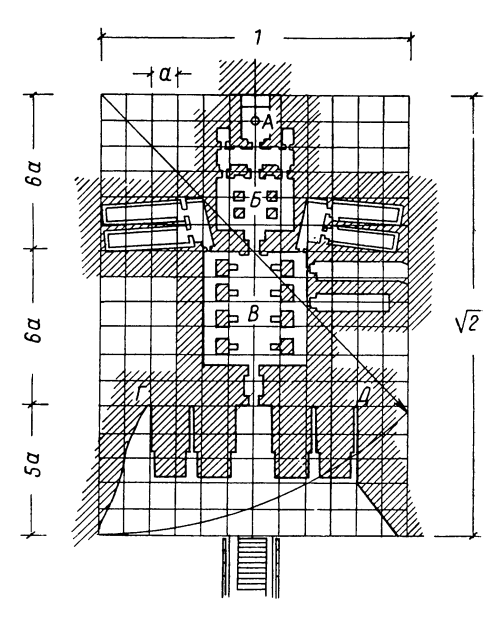
Одним из памятников Нового царства, в котором применено построение по простым числам, является большой храм в Абу-Симбеле. Его внутренняя часть, врытая в скалу, вписывается в квадрат, а весь план храма с открытой передней площадкой имеет размеры, соответствующие отношению стороны квадрата к его диагонали — 1 : 1,4142 (рис. 160 и 161).

Главную роль в пропорциях храма играют, однако, арифметические отношения простых чисел. Сторона основного квадрата, т. е. глубина храма от первой двери до конца святилища, разделена на 12 частей (следует вспомнить, что сумма сторон «священного» египетского треугольника 3+4+5 = 12) . Одна двенадцатая глубины является модулем а и равна ширине святилища А. Ширина зала Б , примыкающего спереди к святилищу, равна 3 модулям, т. е. 3а, а ширина переднего зала В — 4 модулям, т. е. 4а. Длина внешней стены за статуями ГД равна 8 модулям.

Глубина открытой площадки перед фасадом равна 5 модулям, что дает всему габариту храма отношение диагонали к основному квадрату с неуловимой в натуре неточностью 17/12 = 1,4166 (отклонение на 0,002).

Возможно, что композиция храма была предварительно установлена при помощи вспомогательной сетки с ячейкой, равной модулю. Такая сетка определяет многие точки плана (например, положение столбов входного зала или часть углов боковых помещений).

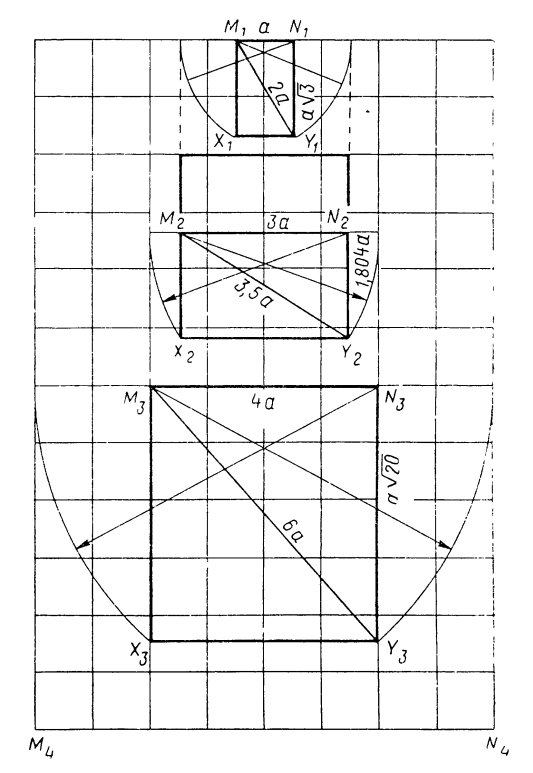
Одновременно с модульными отношениями применен прием нахождения длины трех последовательно увеличивающихся залов (А, Б, В) путем нанесения симметрично расположенных (двусторонних) засечек, исходящих в каждом отдельном случае из ширины последующего (большего) зала и, наконец, из ширины фасада за статуями. Этот прием показан на рисунке 161. Точки М₁, М₂, М₃, М₄ заданы заранее; точки Х₁, Y₁, Х₂, Y₂, Х₃, Y₃ определяются путем нанесения указанных на рисунке засечек.

Так, в святилище А при его ширине в один модуль получается при помощи засечки заданная диагональ, равная 2 а, и, как следствие, его длина равна √3(^√3/₁ = 1,732).

Отношение сторон гипостильного зала Б получается при этом весьма близким к отношению 3/5 с ошибкой, трудно уловимой в натуре: 1,804/3 = 0,601.

Входной зал при его ширине в 4а и заданных диагоналях 6а образует уже знакомый прямоугольник с отношением сторон ^4а/_2а√5 = ⁴/_2√5 = ²/_√5 = ¹/_1,118 (см. рис. 136)

Отношение меньшей его стороны к диагонали равно 2/3, следовательно, этот прямоугольник хорошо включается в систему кратных чисел. При откладывании диагоналей (на продолжении меньшей его стороны) при помощи засечек, указанных на рисунке, получается удвоение меньшей стороны. Иррациональный прямоугольник 1/√3, примененный в святилище, дает в тех же условиях утроение меньшей стороны.

Следует отметить, что в архитектуре Нового царства при осевых симметричных композициях преимущественно применялась засечка диагоналей одинаково по обе стороны той или иной формы, так как применение в Древнем царстве диагональной засечки с одной стороны вызывалось смещением центрального объема с осей ансамбля (как, например, в ансамбле Саккары).

Благодаря приему, по которому пропорции помещения определялись приравниванием его диагонали к определенной части ширины большего помещения с заранее заданными размерами, композиционное построение здания производилось с полным согласованием целого и его частей и, вероятно, в направлении от целого к части (в противоположность архаическому периоду). Составление предварительных схем в этом случае было, очевидно, обязательным. Упомянутый выше чертеж на папирусе Нового царства подтверждает это.

Дошедшие до нас египетские планы очень упрощены и почти не имеют цифр. Остается предположить, что разбивка здания делалась или по ориентировочным схемам и была возможна лишь при постоянном, каноническом приеме построения пропорций, или при непосредственном участии архитектора в постройке.

Шуази в своей «Истории архитектуры» дал анализ одного из самых ранних храмов Нового царства — храма Аменхотепа на о. Элефантина, указав часть отношений, примененных в этом памятнике.

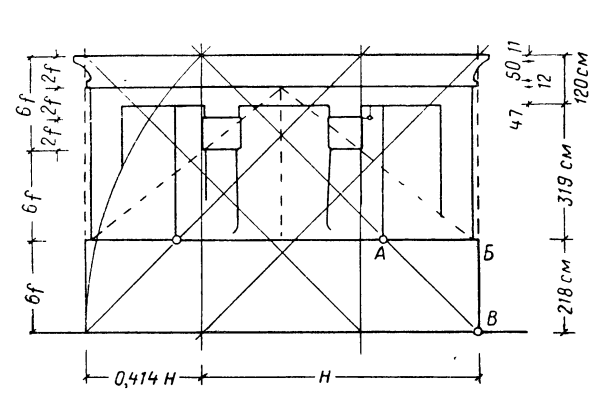
Общая высота здания, по Шуази, делится натри равные части: 1) цоколь; 2) ствол колонны; 3) верхняя часть здания до основания капители (см. рисунок 162, деления в левой части чертежа). Последняя часть делится в свою очередь также на три части: 1) капитель, 2) абака и архитрав и 3) карниз. Высота каждого подразделения выражается целым числом в единице меры, равняющейся одному египетскому футу (36 см), и точно соответствует двум таким футам. «Мы находим здесь, — говорит Шуази, — одновременно простые отношения и целые числа; в этом вся сущность пропорций».

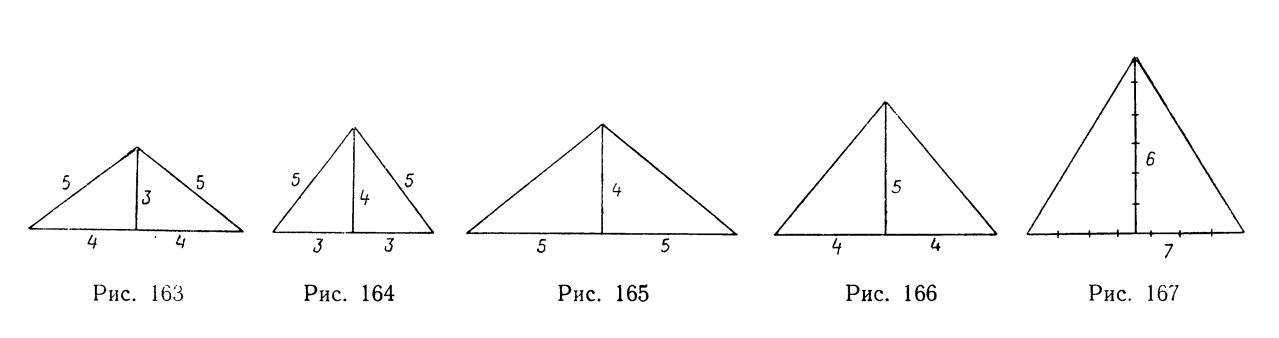
Шуази правильно указал, что при установлении пропорций египтяне часто пользовались треугольниками с отношением сторон 3 : 4 : 5 или треугольниками, которые составляются различными сочетаниями сторон, выраженных числами 3, 4 и 5 (рис. 163-166).

Шуази указал на применение в элефантинском храме треугольника с отношением высоты к основанию 4:10, производного от «священного» треугольника 3 : 4 : 5 (см. рис. 165).

Далее Шуази указывает, что египтяне «из простых отношений предпочтительно пользовались такими, которые совпадают с геометрическими построениями... Фактически метод треугольника (графический) и метод модульных отношений (арифметический) дают почти совпадающие результаты, и в пределах обычных приближений применение треугольников дает простые отношения размеров. Следовательно, оба метода, несмотря на то что их часто противопоставляли друг другу, дают одинаковые результаты. Нужна исключительная точность постройки и точнейшие способы измерения ее частей, чтобы установить, что именно было положено в ее основу — арифметический ли расчет или геометрические комбинации треугольников. При построении равностороннего треугольника или треугольника, высота которого равна 6/7 основания, линии их совпадают»

6/7 = 0,857; √3/2 = 0,866

Шуази, правильно указав на совместное применение и относительную согласованность графического и арифметического методов, не уловил, однако, более древнего способа построения по диагонали, который продолжал применяться в Новом царстве и иногда почти совсем вытеснял кратность по простым числам.

Так, в том же храме на о. Элефантина габарит фасада построен в отношении стороны квадрата к его диагонали (см. рис. 162), а ширина святилища определена пересечением диагонали большого квадрата с верхней линией цоколя (т. е. ширина обходной галереи АБ равна высоте цоколя БВ).

Отношение сторон плана всего храма Аменхотепа установить нельзя. Определенное по чертежам фасадов, оно близко к 3 : 4 (точно 0,748), а определенное по чертежу плана близко к отношению стороны квадрата к его диагонали (на плане не хватает ряда цифр); толщина стен святилища составляет ¹/₄ пролета. План самого святилища с его стенами дает неясное отношение (0,652), близкое к ²/₃, может быть вследствие того, что диагональ святилища равна всей ширине храма. Совместное употребление при построении пропорций простых чисел и диагональных построений, естественно, дает место случайным отношениям.

Золотое сечение в данном памятнике не обнаруживается. Близко к нему стоит отношение антаблемента к высоте колонны ^{1,20 м}/_{3,19 м} = 0,376. Эта величина дает с отношением золотого сечения 0,382 разницу в 0,006. Однако с отношением целых чисел 3/8 (0,375) оно дает меньшую разницу — 0,001.

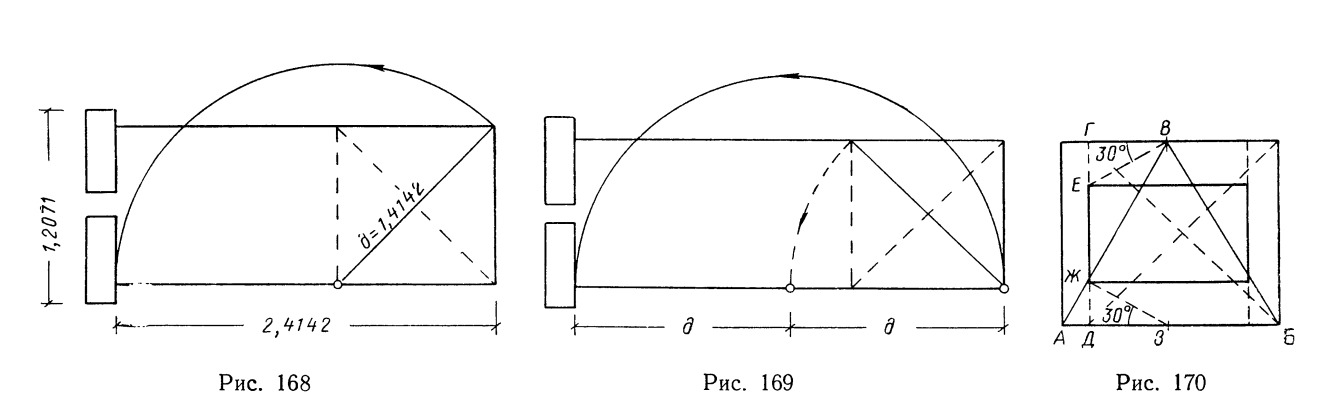
В обычном типе храма Нового царства применяется двойное построение — по модулю и по диагоналям. Однако здесь модуль имеет меньшее значение, и основным приемом построения пропорций являются диагонали, определяющие основные габариты зданий. Так, очень часто внешний габарит храма получается следующим образом. Если на внешней ширине храма построить квадрат, то его диагональ, прибавленная к стороне этого квадрата, определяет длину храма (рис. 168).

Пилон или включен в полученный прямоугольник ¹/_2,4142 или примыкает к нему. При этом длина пилона обычно равна половине длины описанного построения ^2,4142/₂ = 1,2071

Реже встречается построение, при котором длина всего храма определялась при помощи двух диагоналей квадратов со стороной, равной ширине храма (Мединет-Абу, рис. 169).

В виде примера можно привести храм Хонсу в Карнаке. Основой построения пропорций этого храма служит обход, окружающий помещение для священной ладьи (рис. 170).

Прямоугольник обхода описан вокруг равностороннего треугольника и имеет пропорции ²/_√3 = ¹/_0,866 (в натуре ^14,884/_12,664 = ¹/_0,864). Расстояние АД от передней стены обхода до входной грани помещения священной ладьи равно разности основания и высоты равностороннего треугольника. Ширина внутренней камеры ЕЖ получена на передней стороне квадрата ГД при помощи прямоугольных треугольников в 30°, приложенных в точках В и З.

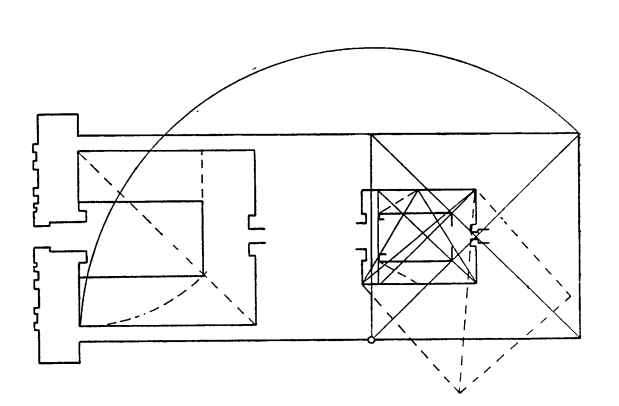
Внешний объем храма построен на диагонали обходной галереи. Ширина наружных стен храма (рис. 171) равна диагонали квадрата, построенного на диагонали обхода.

Наконец, диагональ последнего большого квадрата засекает внутреннюю сторону пилона, определяя таким образом длину храма (см. рис. 168). Ширина пилона равна половине этой длины в натуре ^{66,57 м}/_{32,832 м} = 2,03. Кроме того, она равна диагонали открытого переднего двора, также весьма близкого к квадрату. Толщина пилона близка к ширине святилища.

Подобные построения наблюдаются почти во всех храмах Нового царства. Пропорции их, однако, часто варьируются.

Большое количество совпадений в пропорциях заставляет предположить, что приемы построения, возникшие на границе архаического периода, превратились затем в каноническую схему и в период Нового царства были обязательны. Жрецы, являвшиеся хранителями этих приемов, связали их с религиозной символикой, а создание правил построения зданий приписали обожествленному впоследствии архитектору Древнего царства Имхотепу, как об этом говорит упоминавшаяся выше надпись на стене храма в Эдфу.

Несомненно также, что построение фасадов и разрезов, как это видно на примере храма на о. Элефантина, подчинялось тем же приемам.

Переход к большим прямоугольникам через диагонали меньших вносил согласованность во все элементы здания. Так, например, длина фасада пилона и ширина первого двора в храме Хонсу находятся в отношении диагонали и стороны квадрата, а величина открытой части двора определяется следующим, меньшим квадратом, т. е. квадратом, диагональ которого равна ширине двора. В Эдфу длина пилона равна диагонали квадрата, построенного на глубине двора.

В такой глубоко проникающей «соразмерности» лежит одна из причин впечатления цельности и четкости образа, которое производят египетские храмы.

Конечно, не следует думать, что облик здания был точно и определенно зафиксирован каноном и не допускал отклонений. Наоборот, каждое здание имеет свой облик и свою систему отношений. Общий для них закон построения был только вспомогательным (и относительно гибким) средством для выявления образа конкретного памятника.

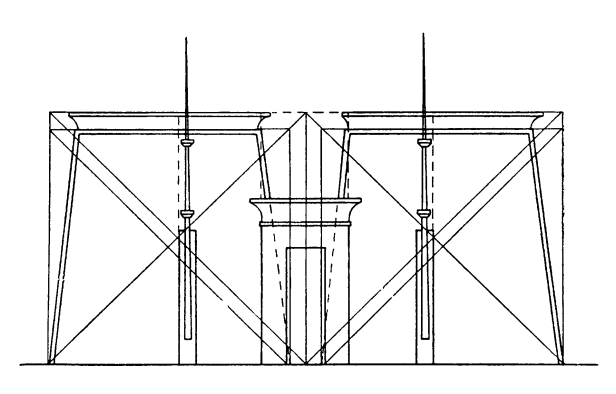
В качестве примера пропорционального построения фасада можно привести схему пилона храма Гора в Эдфу (рис. 172).

Весь объем пилона вписан в два квадрата. Композиция флагштоков вписана в центрально расположенный один квадрат со стороной, равной высоте пилона.

Если продолжить до земли линии внутренних граней башен пилона (частично закрытых порталом), то каждая из двух башен (без карниза) впишется в меньший квадрат. Боковые грани среднего портала определяются пересечением наклонных стен пилонов с верхней линией карниза. Высота свободного промежутка над порталом равна ширине портала (квадрат).

Пилон храма в Эдфу построен в эпоху греко-римского владычества в Египте. Однако в простой схеме его пропорций, сводящейся к квадратам, не чувствуется эллинистических влияний; наоборот, видны отрицание новых веяний и возврат к старым, архаическим приемам.

Более сложными по построению, чем пилоны, были фасады самих храмов.

Передний зал храма Гатор в Дендера может служить примером одной из наиболее сложных композиций этого рода. Основным приемом здесь является применение диагонали квадрата.

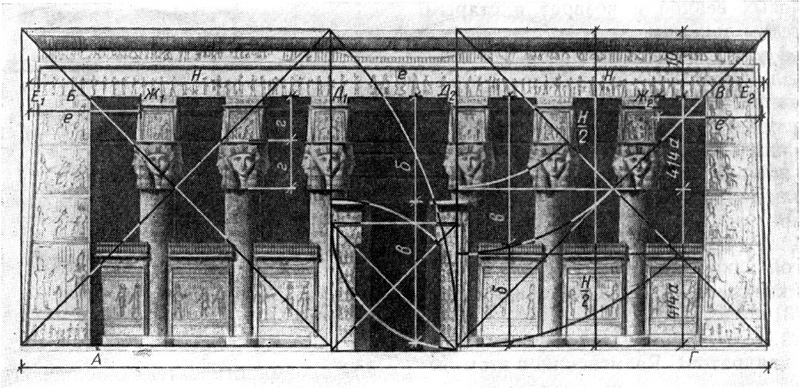
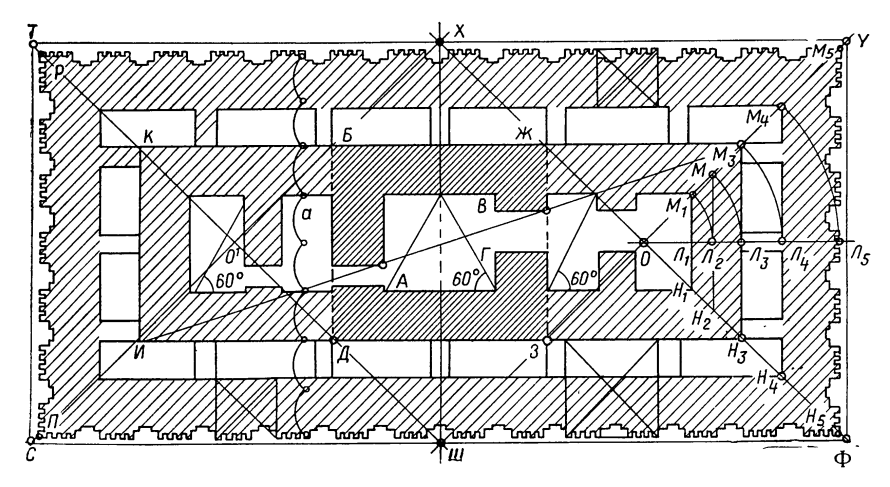
Габарит фасада (без цоколя) дает отношение 1 : 2,414, т. е. состоит из квадрата и прямоугольника, высота которого равна стороне квадрата, а длина — его диагонали (рис. 173).

Вырез АБВГ в стене дает отношение 2 : 5 (десять квадратов). Размещение в этом вырезе осей второй и пятой колонны определено большим квадратом со стороной, равной всей высоте храма.

Положение краев двух центральных колонн фасада (точки Д₁ и Д₂) определяется той же величиной Н (стороной большого квадрата), отложенной от края наклонных стен по нижней линии архитрава (Д₁Е₁ = Д₂Е₂ = Н).

Остаток Д₁Д₂ между средними колоннами, отложенный от точек Е₁ и Е₂ определяется положение крайних колонн Ж₁ и Ж₂.

Высота всего ордера делится на две равные части по нижней линии капители. Высота антаблемента относится к высоте капители как сторона квадрата к диагонали, т. е. ¹/_√2 = ¹/_1,414. Капитель вписана в два вертикально расположенных квадрата и делится пополам по низу тяги над головой Гатор.

Пропорции и членения антаблемента сходны с пропорциями капители с соответствующим уменьшением (на 0,707).

В членении высоты интерколумниев повторяется то же отношение стороны квадрата к его диагонали (¹/_1,414) и притом в обратном направлении, а именно: высота портала относится к высоте сквозного пролета над ним как ^1,414/₁; отношение же высоты стенок в боковых интерколумниях к высоте сквозных пролетов над ними равно ¹/_1,414. Иными словами, высота портала равна высоте пролета над стенками. Самый портал членится в том же отношении: высота его проема относится к общей его высоте как ¹/_1,414.

На фасаде храма в Дендера совсем не заметна арифметическая кратность. Все его пропорции мастерски построены на иррациональном отношении ¹/_√2.

Из проведенного анализа пропорций можно сделать несколько выводов.

Во-первых, выясняется различие приемов пропорционирования, применявшихся в различные эпохи египетской истории. Наиболее древними методами были применение системы диагоналей и метод последовательно увеличивающихся квадратов и в связи с этим пользование иррациональными величинами (включая сюда отношение «функции» 1,118).

В дальнейшем оперирование диагональю полуквадрата приводит в отдельных случаях к применению пропорций группы «золотого сечения». А несколько позже развиваются методы пропорционирования при помощи целых чисел. Наконец, в последующий период все эти способы существуют совместно, с преобладанием, однако, самого древнего приема. (Пропорция золотого сечения встречается редко и не характерна для Древнего Египта. Возможно даже, что это отношение не было тогда осознано и приведено в систему, несмотря на частое употребление диагонали полуквадрата).

Во-вторых, обнаруживается зависимость выбираемого метода пропорционирования от конкретных условий места. Так, в большом храме Абу-Симбела невозможность осуществить в натуре засечки диагоналей внутри скалы, вероятно, заставила применить метод целых чисел.

В-третьих, выбор пропорций определялся рядом художественных факторов: величиной здания, его назначением, требуемым впечатлением торжественности, легкости, сложности, суровости и т. д. В том же храме в Абу-Симбеле на выбор метода пропорций, вероятно, повлияло преобладающее значение скульптуры в облике сооружения. Как указано выше, применение модульного метода было, согласно утверждению Дионисия Галикарнасского, характерным приемом египетской скульптуры.

Наконец, выявляется социально-историческая обусловленность приемов художественной композиции. В период роста египетского государства возникают и определяются новые системы. В период же упадка применяются старые, канонические приемы. В позднем пилоне храма в Эдфу, сооруженном в период чужеземного владычества, выбран самый элементарный архаический способ пропорционирования путем простых квадратов. А на стене памятника делается надпись, оправдывающая выбор ссылкой на священную книгу древнего архитектора Имхотепа.