Глава «Задача Евпалина» книги «Зарождение зодчества». Глазычев Вячеслав Леонидович. Стройиздат. Москва. 1983

Как было обещано в начале книги, мы завершим её одной из множества задач, успешно решавшийся древними. Это «поздняя» задачка (середина VI в. до н.э.), но и ранее решались не менее сложные. Так, когда строились первые египетские пирамиды, царь месопотамского города Лагаш по имени Энтемена (его безымянные инженеры, разумеется) связывает Тигр и Евфрат судоходным каналом на уровне 33-й параллели. А точно выверить ориентацию пирамид по странам света? а выверить горизонтальность основания такой искусственной горы? Обо всех подобных задачах можно писать подробные книги. Мы ограничимся одной — для примера. Итак, тиран острова Самос Поликрат поручил архитектору Евпалину ³⁹ пробить водопровод от источника, лежащего по другую сторону горы Кастро, чтобы городу хватало воды и для питья, и для омовений. Не требовалось особой мудрости, чтобы понять; если пробивать туннель с обоих концов, время сооружении сократится вдвое. Но ведь из точки А не видно точки Б!

39. Вплоть доя середины XVII в. архитектор был и универсальным инженером-строителем. Зная, что Евпалин и другие зодчие его времени решали такие задачи, как та, что приведена в книге, легче понять, какими широкими были познания древнего мастера, каким изощренным было его умение. Опыт, накопленный веками решения жизненно необходимых инженерных задач, и в частности, опыт геометрических построений воплощен и в тонких расчетах, на которых зиждется непреходящая красота Парфенона, смелость мостов-акведуков, построенных римлянами, дерзость строителей средневековых соборов.

Сегодня такая задача решается просто, поскольку вся Земля опутана сетью геодезических координат, к узлам которой можно «привязаться», ибо они обозначены на место, а с помощью точного барометра легко определить высоту точек А и Б над уровнем моря. Но ведь у Евпалина не было барометра, не было точной карты, и всё же он решил задачу: оба туннели встретились почти точно — «колено» в месте встречи не более полуметра при более чем километровой длине туннеля.

Добавим, что для решения задачи нужно меньше, чем даёт школьный учебник геометрии. Ещё бы! Евклид должен был родиться на свет ещё только через три сотни лет, а юный Пифагор ещё только учился в это время у египетских жрецов тайно «египетского треугольника», у которого при сторонах З, 4 и 5 частей обязательно будет точный прямой угол.

Задача Евпалина изрядно волновала древних, и знаменитый Герон Александрийский (тот самый, чья первая паровая турбинка и множество разных автоматов) в своем трактате «Диоптр» дал своё решение (рис. 2). Герон даже написал с гордостью: «Если туннель делать таким образом, то работники встретятся». Увы, Герон не обратил внимания на то, что главное — направление пунктирной линии — взято неизвестно откуда.

К тому же следует иметь в виду, что при умножении числа измерений медленно, но верно нарастает ошибка, а для того, чтобы получить погрешность в полметра на километр длины, построение должно быть совершенно точным.

***

Вот наиболее правдоподобный вариант. Самос времен Поликрата был теснейшим образом связан с Египтом (Пифагор тоже ведь родом с острова), а египтяне должны были издавна освоить точную работу с угломерными инструментами. По рельефу на карте видно, что есть по крайней мере дне точки (С и Д), с которых можно увидеть человека с шестом (рис. 3), стоящего у источника в точке А и у запроектированного вылета туннеля в точке В. Дальше нужна была только тщательная, повторенная для верности несколько раз, работа с астролябией, показанная на нашем рисунке.

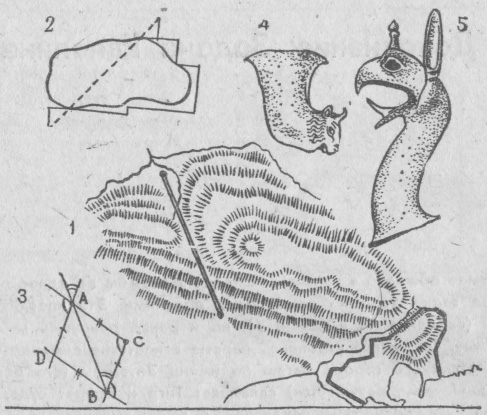Ситуационный план туннеля Евпалина, на острове Самос (1); рисунок из «Диоптра» Герона Александрийского, считавшего, что он определил метод работы Евпалина (2); наша реконструкция задачи Евпалина (3): на ситуационном плане видно, что с вершины горы Кастро можно видеть одновременно точки входа и выхода туннеля, что позволяет точно измерить угол между вспомогательными отрезками (с конца маленького хребта слева можно было произвести проверочное измерение). Изображения сосуда (4) и химеры (5) помогают понять, что когда Евпалин прокладывал туннель, а Пифагор учился в Египте, культура Греции ещё не высвободилась от мощного влияния соседей с юго-востока.

Сложнее другое: как определить точку B или, что то же самое, угол наклона туннеля, по дну которого был прорезан собственно водопровод — узкая и глубокая щель в скале? Но и вероятный ответ на этот вопрос, и то, каким образом удалось сохранить точность направления, все дальше углубляясь под гору, и как Евпалин решил проблему вентиляции... я оставляю работе воображения тех, кому она даёт удовлетворение.

Когда Пифагор постигал египетскую математическую мудрость, столицей Египта был город Саис. Саисские фараоны проявляли живейший интерес к своим далёким предшественникам. Заново были расчищены подземные галереи великих пирамид, восстановлены разграбленные в незапамятные времена гробницы, поставлены на место каменные «замки», закрывающие входы. На восстановленных стенах саисские жрецы оставили письмена:

«Боги, что издревле покоятся в пирамидах,
их благородные слуги, закрытые в пирамидах,
те, кто строил дома, — больше нет их домов.
Что же случилось с ними?
Я слушал беседы Имхотепа и Хардедефа,
чьи слова до сих пор повторяют люди.
Где же дом их теперь?
Рухнули стены домов их — больше нет их домов,
будто их и не было никогда...»

— Так пели жрецы Саиса, отплывая в барках вниз по Нилу после паломничества в Гизе, Санкара, Медум. К счастью, жрецы ошибались: минуло ещё 25 веков, но интерес к мыслям и трудам древних строителей не угас. Напротив, учёные составили уже почти полный поименный список архитекторов, живописцев, скульпторов, их подмастерьев, даже носильщиков и водоносов. Мы знаем, кто они были, как жили — меньше всего мы знаем о том, как они мыслили. Пытаясь разобраться в этом, исследуя самые ранние шаги становления зодчества, мы узнаем многое о себе самих, ведь их знание продолжает жить — в нас.